2. Основные понятия теории графов. Связные графы. Изоморфизм графов. Эйлеровы и гамильтоновы графы. Деревья.
Граф – множество точек (вершин), соединяемых линиями (ребрами). Вершины, дуги и ребра являются элементами графа.
Маршрут – чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершинами, такая, что каждое ребро в нем соединяет только те вершины, между которыми оно стоит.
Цепь – маршрут, в котором нет повторяющихся ребер.
Простая цепь – маршрут, в котором нет повторяющихся вершин (кроме первой и последней).
Цикл – если в простой цепи первая и последняя вершины совпадают.
Связный граф – если любая вершина достижима из любой другой вершины. В противном случае – несвязный. Несвязный граф распадается на несколько частей, каждая из которых является связным графом. Эти части называются компонентами связности.
Циклическое ребро – если оно входит хотя бы в один цикл графа. В противном случае – ациклическое.
Изоморфизм. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей.
Покажем, что следующие два графа изоморфны.

Действительно, отображение a - e, b - f, c - g, d - h, являющееся изоморфизмом легко представить как модификацию первого графа, передвигающую вершину d в центр рисунка.
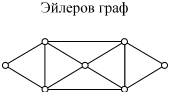
Эйлеровым путем в графе называется путь, содержащий все ребра графа. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа.
Связный граф ![]() называется эйлеровым, если существует
замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой
цепью. Отметим, что в этом определении требуется, чтобы каждое ребро
проходилось только один раз. Если снять ограничение на замкнутость цепи, то
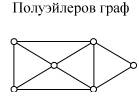
граф называется полуэйлеровым, при этом каждый эйлеров граф будет
полуэйлеровым.
называется эйлеровым, если существует
замкнутая цепь, проходящая через каждое его ребро. Такая цепь называется эйлеровой
цепью. Отметим, что в этом определении требуется, чтобы каждое ребро
проходилось только один раз. Если снять ограничение на замкнутость цепи, то
граф называется полуэйлеровым, при этом каждый эйлеров граф будет
полуэйлеровым.
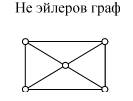
Гамильтонов цикл – цикл, проходящий через все вершины графа.
Гамильтонов граф – граф, имеющий хотя бы один Гамильтонов цикл.
Связный граф является Гамильтоновым, если число его вершин N, а валентность каждой вершины больше, чем N/2.
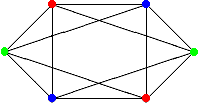
Раскраской графа (правильной) называется приписывание цветов его вершинам, такое что никакие две соседние вершины не окрашены в одинаковый цвет.
На следующем рисунке показана правильная раскраска.
 |
Теорема Кёнига о покрывающих линиях. Пусть имеется некоторая матрица, в которой все элементы равны либо нулю, либо единице. Будем словом линия обозначать либо строку, либо столбец в данной матрице. Две единицы в матрице будем называть независимыми, если они не находятся на одной линии. Произвольный набор единиц будем называть набором независимых единиц, если любые две единицы в наборе независимы. Наконец, набор линий в данной матрице будем называть покрывающим, если каждая единица матрицы принадлежит хоть одной линии набора. Теорема Кёнига утверждает: максимальное число независимых единиц матрицы равно минимальному числу линий, составляющих покрывающий набор. Существует знаменитая теорема Эйлера о раскраске плоских графов: всякий плоский граф можно раскрасить пятью цветами. Нельзя не отметить, что реально пока не найдено ни одного плоского графа, который нельзя было бы раскрасить четырьмя цветами. Только основные комбинаторные конфигурации.
Дерево – связный граф, не содержащий циклов.
Свойства деревьев.
1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.
2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.
3. Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.