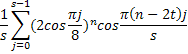1. Основные комбинаторные конфигурации. Бином Ньютона. Биномиальные коэффициенты. Основные тождества с биномиальными коэффициентами.

Комбинаторные конфигурации

Размещения с повторениями

Общее число размещений с повторениями из n по k равно

|Х₁×Х₂×…×Х_k|=n^k

Размещения без повторений

Общее число размещений без повторений из n по k равно

=n(n-1)…(n-k+1)=n!/(n-k)!

Перестановки

Число перестановок из n элементов равно

Р_n= n!

Сочетания

Число сочетаний из n по k равно

= n! / k!·(n-k)!

Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

где

— биномиальные коэффициенты, n — неотрицательное целое число.

В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона (1 + x)ⁿ по степеням x. Коэффициент при x^k обозначается (n/k) (иногда ):

В комбинаторике биномиальный коэффициент (n/k)интерпретируется как число сочетаний из n по k, равное количеству всех подмножеств (выборок) размера k в n-элементном множестве.

начение биномиального коэффициента (n/k)определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:

для $0\leqslant k\leqslant n$ ;

(n/k)=0 для k < 0 или $0\leqslant n<k$ ;

для $n<0\leqslant k$ ,

где n! и k! — факториалы чисел n и k.

Тождества

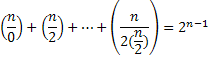
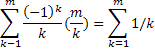
Мультисекция ряда (1 + x)ⁿ даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t $(0\leqslant t<s)$ в виде замкнутой суммы из s слагаемых: