3. Численное интегрирование. Квадратурная формула прямоугольников. Формулы Ньютона-Котеса. Формула трапеций. Формула Симпсона.

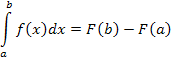
Квадратурные формулы

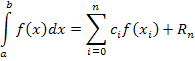
– узлы,– весовые множители, – погрешность

сл-но

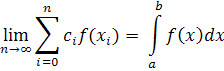
Метод прямоугольников

– шаг интегрирования

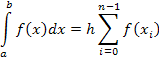
Формулы Котеса.

числа H_i - коэффициентs Котеса, вычисляются как интегралы от соответствующих многочленов, стоящих в исходном интерполяционном многочлене для подынтегральной функции при значении функции в узле x_i = a + ih (h = (b − a) / n — шаг сетки; n — число узлов сетки, а индекс узлов $i=0 \ldots n$ ).

$r_n(f)\,$ — погрешность метода, которая может быть найдена разными способами. Для нечетных $n \geqslant 1$ погрешность может быть найдена интегрированием погрешности интерполяционного полинома подынтегральной функции.

Частными случаями формул Котеса являются: формулы прямоугольников (n=0), формулы трапеций (n=1), формула Симпсона (n=2), формула Ньютона (n=3) и т. д.

Метод трапеции

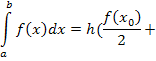
Метод Симпсона

n=2m (количество отрезков четное)
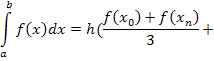