Статистическая гипотеза – гипотеза о виде закона распределения случайной величины, о параметрах этого распределения или о соотношении этих параметров.

Выдвигается нулевая гипотеза H₀, подлежащая проверке. Подбирается критическое событие s с известной малой вероятностью a, по которой делают вывод принимать или отвергать гипотезу H₀. H₀ отвергают, если событие S происходит, при этом существует риск ошибки первого рода: отвергнуть правильную гипотезу. Вероятность этой ошибки (a) называется уровнем значимости гипотезы H₀. Или H₀ принимается, если событие S не происходит. Возникают два вопроса: о единственности события S, о вероятности другой ошибки – принять неверную гипотезу. На эти вопросы можно дать ответ: если верно следующее предположение – когда неверна гипотеза H₀ всегда справедливо другое предположение H₁  - альтернативная или конкурирующая гипотеза.

Значение критерия, полученного по эмпирическим данным принято называть наблюдаемым значением, а точки на числовой оси, разделяющие область принятия гипотезы и критические области называются критическими значениями.

Задача проверки гипотезы H₀ сводится к отысканию значения K_набл и сравнению этого значения с К_критич. Точки, отделяющие критическую область от области принятия называются критическими точками.

Для проверки нулевой гипотеза используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Ее обозначают t если она распределена по закону Стюдента, X² - по закону "хи квадрат", F- по закону Фишера, G - по закону Кохрэна. Обозначим эту величину К

Статистическим критерием (или просто критерием) называется случайная величина К, служащая для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением (К_набл) называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества; одно из них содержит значения критерия, при которых нулевая гипотеза отверга­ется, а другое - при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называ­ют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформули­ровать так: если наблюдаемое значение критерия принадлежит критичес­кой области - гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы -  гипотезу принимают.

Поскольку критерий К - одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами, и, следовательно, существуют точки, которые их разделяют.

Критическими точками К_кр называют точки, отделяющие критичес­кую область от области принятия гипотезы.

Различают, одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую нера­венством К>К_кр , где  К_кр- положительное число.

Левосторонней называют критическую область, определяемую нера­венством К<К_кр , где  К_кр- отрицательное число.

Односторонней называют правостороннюю или левостороннюю крити­ческую областью.

Двусторонней называют критическую область, определяемую неравенствами  K<K1, K>K2, где К2>К1. 

Критерий Пирсона.

Критерий универсален по отношению к любому распределению.

Критерий является квадратичной формой вида:

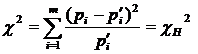p_i- эмпирические частоты,p(штрих-итое)_i- теоретические частоты

Полученное значение сравнивается с критическим значением при заданном уровне значимости (a) и числе степеней свободы k=s-1, где s – число групп (интервалов).

Если < - нулевую гипотезу не отвергаем.

Для других распределений K=S-m-1, где m- число параметров, рассчитанных по данным выборки.

Для равномерного распределения m=0

Для распределения Пирсона m=1.