1. Формализация понятия алгоритм. Тезис Тьюринга-Черча

Теория алгоритмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. Задачи – формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.

Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных.

Пусть D – область (множество) исходных данных задачи, а R – множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение D --> R. Поскольку такое отображение может быть не полным, то вводятся следующие понятия:

Алгоритм называется частичным алгоритмом, если мы получаем результат только для некоторых d є D и полным алгоритмом, если алгоритм получает правильный результат для всех d є D.

Варианты словесного определения алгоритма принадлежат российским ученым А.Н. Колмогорову и А.А. Маркову

(Колмогоров): Алгоритм – это всякая система вычис-лений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.

(Марков): Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.

Отметим, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:

алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.

Другие формальные определения понятия алгоритма связаны с введением специальных математических конструкций (машина Поста, машина Тьюринга, рекурсивно-вычислимые функции Черча) и постулированием тезиса об эквивалентности такого формализма и понятия «алгоритм».

Машина Тьюринга

Алан Тьюринг 1936 статья «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.

Предыстория создания этой работы связана с формулировкой Давидом Гильбертом на в 1900 году неразрешенных математических проблем. Одна из них – задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» - нахождение общего метода, для определения выполнимости данного высказывания на языке формальной логики.

Статья Тьюринга давала ответ на эту проблему - вторая проблема Гильберта оказалась неразрешимой.

Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.

Формально машина Тьюринга может быть описана следующим образом: Пусть заданы:

конечное множество состояний – Q, в которых может находиться машина Тьюринга;
конечное множество символов ленты – Г;
функция (функция переходов или программа), которая задается отображением пары из декартова произведения Q x Г (машина находится в состоянии 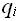и обозревает символ ) в тройку декартова произведения Q х Г х {L,R} (машина переходит в состояние 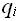, заменяет символ на символ 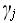и передвигается влево или вправо на один символ ленты) – Q x Г-->Q х Г х {L,R}
один символ из Г-->е (пустой);
подмножество 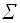є Г --> определяется как подмножество входных символов ленты, причем е є (Г- );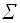
одно из состояний – 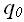є Q является начальным состоянием машины.

Решаемая проблема задается путем записи конечного количества символов из множества є Г – Si є на ленту:

….

после чего машина переводится в начальное состояние и головка устанавливается у самого левого непустого символа – , после чего в соответствии с указанной функцией переходов (,)-->(,, L или R) машина начинает заменять обозреваемые символы, передвигать головку вправо или влево и переходить в другие состояния, предписанные функций переходов.

Остановка машины происходит в том случае, если для пары (,) функ-ция перехода не определена.

Алан Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Это предположение известно как тезис Черча–Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины). Следовательно, он может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.