Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.

Имеются какие-то переменные и функция этих переменных , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.

Линейное программирование характеризуется тем, что

а) функция

является линейной функцией переменных ;

б) область G определяется системой линейных равенств или неравенств.

Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ — раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями. В экономике это соответствует тому, что результаты (эффективность) возрастают или убывают непропорционально изменению масштабов использования ресурсов (или, что то же самое, масштабов производства): напр., из-за деления издержек производства на предприятиях на переменные и условно-постоянные; из-за насыщения спроса на товары, когда каждую следующую единицу продать труднее, чем предыдущую; из-за влияния экстерналий (см. Внешняя экономия, внешние издержки) и т. д.

В краткой форме задачу Н. п. можно записать так:

F (x) → max при условиях g (x) ≤ b, x ≥ 0,

где x — вектор искомых переменных; F (x) — целевая функция; g (x) — функция ограничений (непрерывно дифференцируемая); b — вектор констант ограничений (выбор знака ≤ в первом условии здесь произволен, его всегда можно изменить на обратный).

Решение задачи Н. п. (глобальный максимум или минимум) может принадлежать либо границе, либо внутренней части допустимого множества.

Иначе говоря, задача состоит в выборе таких неотрицательных значений переменных, подчиненных системе ограничений в форме неравенств, при которых достигается максимум (или минимум) данной функции. При этом не оговариваются формы ни целевой функции, ни неравенств. Могут быть разные случаи: целевая функция нелинейна, а ограничения линейны; целевая функция линейна, а ограничения (хотя бы одно из них) нелинейны; и целевая функция, и ограничения нелинейны.

 

Штрафных функций метод, метод сведения задач об отыскании условного (относительного) экстремума функций к задачам отыскания безусловного (абсолютного) экстремума.

Основная идея методов штрафных функций состоит в преобразовании задачи условной оптимизации в задачу безусловной оптимизации или в последовательность задач безусловной оптимизации.

Пусть решается задача условной оптимизации

               z = f(X) → min,

               cj(X) > 0, j = 1, 2, . . . , m.

Построим функцию штрафа P(X):

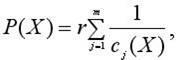
где  r>0 - коэффициент штрафа.

Тогда можем записать новую целевую функцию в виде

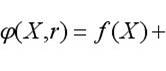
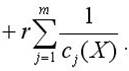
Если X принимает допустимые значения, т.е. cj(X)>0, то φ(X,r) принимает значения, которые больше f(X), но разность можно уменьшить за счет того, что r может быть очень малой величиной. Но если X хотя и допустим, но очень близок к границе (хотя бы одна из функций cj(X) близка к нулю), то значения функции P(X), а значит, и функции φ(X,r) становятся очень большими. Таким образом, P(X) создает "гребень с крутыми краями" вдоль каждой границы области ограничений. Следовательно, если поиск начинается из допустимой точки и производится поиск минимума функции φ(X,r) без ограничений, то минимум будет достигаться внутри допустимой области для задачи с ограничениями. Полагая r достаточно малой величиной для того, чтобы влияние P(X) было малым в точке минимума, можно сделать точку безусловного минимума функции φ(X,r) сколь угодно близкой к точке условного минимума функции f(X). В общем случае, решая последовательность задач безусловной оптимизации с уменьшающимся r, можно получить приближенное решение задачи условной оптимизации. На этом основан так называемый SUMT-метод Фиакко и Маккормика (метод последовательной безусловной оптимизации).

Штрафная функция, приведенная выше называется барьерной. Другой вид барьерной функции (логарифмическая барьерная функция):

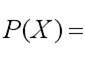
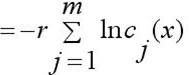
Эта барьерная функция вообще не определена за пределами допустимой области.

Штрафные функции могут иметь и другой вид. Например, для ограничений-равенств имеем:

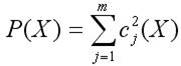 - квадратичная штрафная функция,

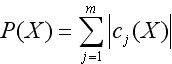 - абсолютная штрафная функция,

 

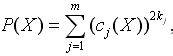
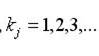 - штрафная функция, позволяющая учитывать "важность" ограничений.

Если же в постановке задачи присутствуют ограничения-равенства (hj(X)) и ограничения-неравенства (gi(X)) одновременно, то штрафная функция может быть записана, например, в виде:

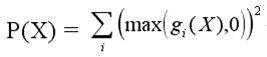
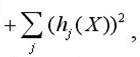
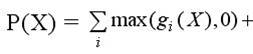
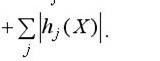
Недостатки метода: определяется только локальный минимум, трудности одномерного поиска (не везде определена функция) не позволяют использовать стандартные методы, плохая обусловленность Гессиана, существенно овражный характер штрафной функции вблизи границы.

Возможные пути преодоления: мультистарт, специальные методы одномерного поиска, использование на предварительных этапах "гибридных" методов в сочетании с алгоритмами, имеющими хорошие свойства локальной сходимости, и овражными алгоритмами.

Метод множителей Лагранжа.

Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях-равенствах. Безусловный и условный экстремумы в задаче Лагранжа. Применение неопределенных множителей Лагранжа сводит задачу оптимизации с ограничениями к задаче.

Метод нахождения условного экстремума функции f(x), где x  приналдежит Rⁿ ? относительно m  ограничений φ_i(x)=0? I меняется от 1 до m

Описание метода

Составим функцию Лагранжа в виде линейной комбинации функции f и функций φ_i, взятых с коэффициентами, называемыми множителями Лагранжа — λ_i:

где .

Составим систему из n + m уравнений, приравняв к нулю частные производные функции Лагранжа  по x_j и λ_i.

Если полученная система имеет решение относительно параметров x'j и λ'i, тогда точка x' может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.